概要
混合正規分布モデル(Gaussian Mixture Model, GMM)を多層化したDeep GMMを提案する.任意の正規分布は,標準正規分布の線形変換によって生成することができる.GMMを一つの標準正規分布から複数の線形変換を通した正規分布の線形和と考えると,この線形変換を層と見なして複数積み上げることによって,いくつもの線形変換を経た正規分布の和としてDeep GMMを定義することができる.多層化によって複雑な特徴を表現することができるほか,少ないデータで実行可能であり,過学習が起きにくい.この論文ではスケーラブルな実装方法も述べられている.
混合正規分布の多層化
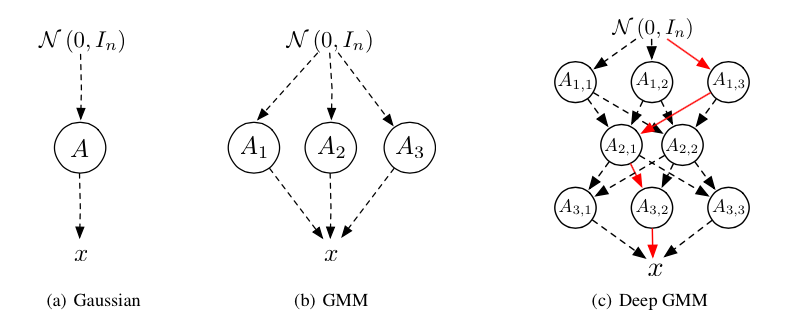
任意の多変量正規分布は,標準正規分布$\mathcal{N}(0,I)$を元にして変数変換$x=Az+b$により生成することができる.その時の多変量正規分布は$p(x)=\mathcal{N}(x|b, AA^T)$と表すことができる.これをFigure 1aのように考えると,混合正規分布はFigure 1bのように線形変換$A_1,A_2,A_3$で生成された正規分布の和として表現することができる.なお,この図はグラフィカルモデルではないので注意.
 (Figure 1: NIPS2014_5227.pdf)
(Figure 1: NIPS2014_5227.pdf)
この要領でFigure 1cのように線形変換の多層化によって複数積み重ねたものが,Deep GMMの基本的な概念となる.$m$番目のレイヤーの$n$番目の線形変換を$A_{m,n}$および$b_{m,n}$で表す.パス$p = (p_1,p_2\dots p_k) \in \Phi $における混合係数を$\pi_p$とすると,$x$の密度関数は以下のように表される.
\( p(x)=\sum_{p\in \Phi} \pi_p \mathcal{N}(x|\beta_p, \Omega_p \Omega_{p}^{T}) \)
このときの$\beta_p$および$\Omega_p$は論文中の数式(2),(3)を参照.基本的に入れ子構造になっている.また,GMMと同様に混合係数$\pi_p$は全体で1になる.このように,正規分布のパラメータが複雑になっている以外はGMMと同じような書き方ができるため,GMMはDeep GMMが単層になった特殊なケースと考えることができる.
EMアルゴリズムを使ったDeep GMM
Deep GMMはGMMと同じくEMアルゴリズムによって最適化する.Eステップでは負担率$\gamma_{np}$を計算し,Mステップではパラメータを更新する.
・Eステップ
負担率$\gamma_{np}$もGMMと同様に以下のように表される.
\( \gamma_{np}=\frac{\pi_p \mathcal{N}(x|\beta_p, \Omega_p \Omega_{p}^{T})}{\sum_{p\in \Phi} \pi_p \mathcal{N}(x|\beta_p, \Omega_p \Omega_{p}^{T})} \)
それぞれのパス$p_1,\dots,p_k$について計算しなければいけないので計算量は増えるけれども,Eステップは個別のデータ点について独立に$\gamma_{np}$を計算すればいいので並列化が可能.また”hard” assignmentで簡略化することもできる.これは,それぞれのデータ点について1つの負担率だけを1,その他を0にする計算方法で,Hard-EMと呼ばれる.
それに加えて,今回はヒューリスティックな手法も導入する.パス$p$はcoordinate ascentで計算する.これは他のパラメータを固定した状態で一つのパラメータ$p_i$だけを最適化し,それを繰り返していくというもの.これだと対数尤度は初期値によって局所最適解に落ちる場合もあるので,warm startで前回のEステップの負担率を利用しつつ3回繰り返す.
.Mステップ
ちょっとココらへんは理解できていないので省略.
評価
Berkeley Segmentation Dataset(BSDS300)を使用して評価.Deep GMMはEステップにおいてHard-EMでヒューリスティックな方法を使い,MステップはLBFGS-Bを1000回まわして実行した.EMアルゴリズム全体の反復回数は100回に固定したが,だいたい少ない回数で十分とのこと.
まずは必要なモデルの複雑さの評価.単層のGMM,2層と3層のDeep GMMにおいて,一番上の層の要素数を増やした時の対数尤度の比較がFigure 4aに示されている.ここでDeep GMMの他の層は要素数5に固定.パラメータ数自体はほぼ同じだが,Deep GMMが良い性能を示した.また,データ自体をダウンスケール化したときの評価でも同様の結果となった.
既存研究との比較として,RNADEやEoRNADE(Ensembles of RNADEs),通常のGMMやSTM(t分布を使った混合分布)でも試した結果,Deep GMMはEoRNADEに並ぶ結果となった.
感想
説明変数の特徴を複数の正規分布だけで表現させて,多層化することにより複雑なモデルを作ろうという考え方は面白い.発想としては,論文中でも述べられてる通りHinton先生のところのFactor Analysisの混合モデルを多層化したものと似ている(1206.4635 Deep Mixtures of Factor Analysers).論文の中では応用例が画像認識のみになっているが,生成モデルが適用できる他のタスクでどれだけ精度が上がるか気になるところ.